Az 1960-as évek közgazdász tudósai az alábbi kérdésekre keresték a választ: Mi történik a tőkepiacon, ha minden befektető a Markowitz-portfólióelmélet szerint dönt? Milyen feltételek mellett lesz egyensúly? Mik a jellemzői ennek az egyensúlynak?
Ezen kérdésekre a válasz William Sharpe, John Lintner és Jack Treynor részéről jött, akik egy máig alkalmazott modellt hoztak létre, mellyel megtudhatjuk, hogy mekkora a kockázati díj, ha a részvényeink nem teljesen függők, vagy épp függetlenek a piactól. Ez a jól ismert modell a CAPM (Capital Asset Pricing modell), azaz a tőkepiaci árfolyamok modellje. Segítségével a befektetők számára kiszámíthatóvá válik a befektetések, részvények elvárt hozama. A módszer alapkérdése, hogy a befektetéskor felvállalt kockázathoz mérten elérhető-e az a minimális mértékű hozam, amelyet egy hasonló befektetésből is megkapnánk.
A modell feltevései az alábbiak:
- Minden befektető kockázatkerülő.
- Minden befektetőnek egy periódusra vonatkozó hasznosságfüggvénye van, amely a hozamszórás terében definiált.
- Tökéletes tőkepiac feltevései fennállnak.
- A befektetői várakozások homogének.
- Van lehetőség kockázatmentes hitelfelvételre, illetve betételhelyezésre (amelyek kamatlába megegyezik).
A feltevések valóban sok tekintetben a valóságtól elrugaszkodott állításokat tartalmaznak. A feltevések egyes feloldásai révén a CAPM-nek más továbbfejlesztéseit is használják (Zéró-béta CAPM, Fogyasztási CAPM, Illikviditási prémium stb.)
A béta, azaz a piaci portfólióval való együttmozgás mértékének (kovariancia) bevezetése révén az alábbi egyenlőséget állapították meg: E(R) = Rf + ß( Rmarket – Rf ), ahol a béta (β) a részvény hozama és a részvénypiaci hozam közötti összefüggést fejezi ki. Értékei:
- β = 1: ha a piaci hozam 1%-kal változik, akkor a részvény hozama is 1%-kal változik.
- ß < 1: ha a piaci hozam 1%-kal változik, akkor a részvény árfolyama kevesebb, mint 1%-kal változik.
- β > 1: ha a piaci hozam 1%-kal változik, akkor a részvény árfolyama több, mint 1%-kal változik.
Rf a kockázatmentes hozamot, Rmarket pedig a piaci kockázatot jelenti.
Tehát minden jól árazott egyedi eszköz várható hozama megegyezik a kockázatmentes hozam, valamint a kockázati prémium piaccal való együttmozgás-mértékével szorzott érték összegével. Ennek egyik levezetése, az SML (security market line), az értékpapírpiaci egyenes ábráján látható:
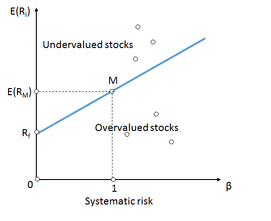
A levezetési folyamatot követően az említett feltételek mellett a tőkepiaci árfolyamok modellje az alábbi tényeket állítja:
- A piaci portfolió és a kockázatmentes befektetés hatékony portfólió.
- Mindegyik befektető hatékony portfóliót (azaz a kockázatmentes befektetés és a piaci portfólió kombinációját) választ magának.
- Ha fenti állítások teljesülnek, akkor a piac egyensúlyban van: a hozamvárakozások és a befektetői portfóliók olyan együttese jön létre, ahol minden befektető portfóliója optimális.
A CAPM-et összefoglalva tehát az alábbi állításokra juthatunk:
- Egyensúlyban a piaci portfólió hatékony, az érintési portfólió a piaci portfólió lesz (fő állítás!).
- Minden befektető a piaci portfóliót tartja optimális kockázatos befektetésnek.
- Minden befektető a kockázatmentes eszköz és a piaci portfólió keverékébe fektet (CML).
- Árazás az SML alapján: E(R) = Rf + ß( Rmarket – Rf ).
- Kockázati prémium a nem diverzifikálható kockázatért cserébe jár.
- Passzív befektetési stratégia hatékony.
Jogosan merül fel a kérdés, hogy a valóságban milyen pénzügyi döntéseknél kerül elő a CAPM használata, és milyen módszerekkel állíthatóak elő a tökéletes árazáshoz szükséges paraméterek. Tőkeköltség-becslés (WACC) során szükségünk van a vállalat rE, azaz a sajáttőke-hozamára, amelyhez CAPM alkalmazható; megbecsülhetjük egyedi tőkepiaci eszközünk (például részvényünk) elvárt hozamát; részvényportfólió összeállításánál rangsorolási szempontként is alkalmazhatóak a megkapott elvárthozam-értékek, illetve vállalatértékelések, projektfinanszírozások részvényopciós piac-vizsgálatnál a diszkontfaktor tökéletes „alapanyagaként” szolgálhat a CAPM-mel kalkulált elvárt hozam értéke.
A következő cikkben betekintést nyerhetünk a gyakorlati alkalmazás módszereibe és fortélyaiba.
Képek: http://www.esan.edu.pe/conexion/actualidad/2016/07/18/capm_principal1.jpg
https://en.wikipedia.org/wiki/Security_market_line
Felhasznált irodalom: Richard A. Brealey, Stewart C. Myers: Principles of Corporate Finance, 2005.



