Káosz…Tegyünk rendet körülötte!

A káoszelmélet születése a 19. század végére nyúlik vissza, de létrejötte a természettudományok sok ágához hasonlóan nem volt szándékos, véletlen felfedezések vezettek el a kiforrásához. A meteorológia fejlődése, a számítási kapacitások javulása, valamint a Naprendszer fizikájának alaposabb modellezése és a pontosabb számítások elvégzése előre jelezte a káoszelmélet térnyerését. Henry Poincaré neves matematikus, fizikus és csillagász, a matematikában elért úttörő eredményei mellett szívesen foglalkozott csillagászati problémákkal is, mint például a háromtest-problémával.

Erre lehet példa egy központi csillag (Nap) körül keringő bolygó (Föld) és az a körül keringő hold (Hold) esete. Lényegében arról van szó, hogy három test egymás gravitációs terében mozog bizonyos kezdeti feltételekkel a Newton-törvények szerint. Poincaré volt az, aki kimutatta tisztán matematikailag, hogy egy ilyen rendszer időbeli fejlődését leíró differenciálegyenlet rendszereknek nem adható meg zárt alakban, analitikusan a megoldása. Ez már önmagában is kimagasló eredményt jelentett Poincaré részéről, de arra is rájött, hogy ha fejlődni hagyjuk ezeket a rendszereket, akkor bizonyos idő eltelte után el fognak egymástól térni. Ez azt jelenti, hogy a három egymás gravitációs terében mozgó test rendkívül érzékeny a kezdeti feltételek megadására, hiszen az idővel ezek nemhogy eltűnnek, hanem fel is erősödnek.

Hasonló sémára bukkant Edward Lorenz amerikai meteorológus és matematikus a Navier-Stokes egyenletek vizsgálatakor a meteorológiai előrejelzésekben. Ezek az egyenletek lényegében a newtoni klasszikus fizikai megfontolásait ültetik át a folyadékok és gázok áramlásainak dinamikai leírásához. Lorenz azzal foglalkozott, hogy számítógép segítségével a légkör egyes pontjaiban megadja az ott lévő részecskéknek a sebességét. A történet érdekes fintora, egyfajta előre kiszámíthatatlan anomáliája volt Lorenz álmossága és talán lustasága, hiszen amíg a gép dolgozott a számításokon, ő elment inni egy kávét, és visszatérve a számítások megpörgetése végett a kiszámított (de kerekített) adatokat táplálta vissza a gépbe. Talán nem a koffein volt ekkor az, ami felébresztette Lorenzet, hanem az, hogy az ötödik tizedesjegyben a kerekítéssel történő számolás nem hogy hasonló, hanem merőben más visszatérési értéket szolgáltatott mint a kerekítés nélküli esetben. A kezdeti feltételekre való rendkívüli érzékenységet kiemelve, Lorenz hozta be a köztudatba azt a túlzó hasonlatot, miszerint egy pillangónak a szárnycsapása akár kavarhat forgószelet is Texasban.

Azonban látni fogjuk, hogy ez nem teljesen van így, de előbb tisztázzuk mit is értünk pontosan a pillangóhatáson, és mik a feltételei annak, hogy egy rendszert kaotikusnak nevezzünk.

Azt mondjuk, hogy a kaotikusság feltétele, hogy a rendszer legyen időben szabálytalan, hosszútávon előre jelezhetetlen a kezdeti feltételekre való érzékenység miatt, valamint hogy képesek legyünk valamilyen fraktálszerkezetet társítani hozzá. Ezeket a tulajdonságokat nézzük meg egy kicsit közelebbről is. Ez a három feltétel általában is fennáll egy kaotikus rendszer esetében, így lehet megkülönböztetni a zajtól, hiszen a véletlenszerűség ebben az esetben a rendszer érzékeny belső dinamikájából ered. Továbbá, a zajban a rengeteg összetevő véletlenszerű viselkedése a nagy számú alkotó részecske egyszerű, de sok kölcsönhatására vezethető vissza (pl. Brown-mozgás). Ezekre a valószínűségszámítás módszereit alkalmazva, nagyléptékben kezelhető és megjósolható következményeket kaphatunk. Káosz esetén azonban pont nem a rendszer számbeli összetettsége számít, és a valószínűségszámítás sem alkalmazható ilyen formában,  mert itt hosszú távon kerül elvesztésre a determinizmus.

Fontos elmondani, hogy a káosz kapcsolata a valószínűséggel máshonnan ered, mint a kvantumelméletben. Itt nem arról van szó, hogy a természetnek egy kardinálisan más, meglepő és új viselkedését fedezték fel, hanem sokkal inkább arról, hogy bizonyos folyamatoknak a nemlinearitása  erősen befolyásolja annak időbeli fejlődését. A káosz lényegében arra mutat rá, hogy egyszerű törvények is vezethetnek olyan bonyolult viselkedésekre, melyeknek az időbeli fejlődése egy idő után nem megjósolható. Így jutunk el oda, hogy a newtoni fizika keretein belül egy rendszerben nem determinisztikus karaktereket fedezhetünk fel. Ilyen rendszerekben a következmények sem egyenesen arányosak az okokkal, ezért mondjuk a rendszert nemlineárisnak és a kezdeti hibákat erősítőnek. Végül, az aperiodicitás azért fontos karakter, mert ha a mozgásnak lennének periodikus szakaszai, akkor az már nem lenne véletlenszerű a további fejlődés során. 

Vegyünk példának egy mágneses ingát, melyet elengedve mozgása során három rögzített mágneshez térhet végső helyzetbe. Meg lehet figyelni, hogy mivel a kezdőfeltételekre rettenetesen érzékeny az ingának a kilendítése, így a látszólag “azonos” helyekről is más-más centrumokba térhet nyugalomba lengése végén. Mozgása során az ingatest véletlenszerűen mozog a három rögzített mágnes erőterében, azonban valamelyikhez biztosan oda fog érni, így azt mondhatjuk, hogy ennek a rendszernek három attraktor (vonzási) pontja van.  De mi is az az attraktor? A fázistér egy olyan szemléltető tér aminek minden pontjához az adott dinamikai rendszernek egy lehetségesen megvalósulható állapota rendelhető. Az attraktorok – mint azt a nevük is mutatja – olyan pontjai ennek a fázistérnek, amelyek mintegy vonzásközpontként működnek bizonyos vonzási tartományokban. Ez azt jelenti, hogy ha a test egy adott vonzási tartományon belül kerül, akkor az ahhoz tartozó attraktorban talál egyensúlyra.

Itt kapcsolódhatunk át a kaotikus rendszerek harmadik ismérvéhez, mégpedig a fraktálszerkezet megjelenéséhez. Ugyanis, ezeknek az attraktoroknak a vonzási tartomány  határai ahogy egymással összefonódnak, kaotikus rendszerek esetében fraktálszerű struktúrát mutatnak.

A fraktálok olyan alakzatok, melyeket tetszőlegesen felnagyítva az önhasonlóságuk folytán nagyobb skálán ismert mintázatok jelennek meg a kisebb részletekben is. Gondoljunk csak bele, hogy milyen érdekesen kapcsolódnak össze a kaotikus rendszerek jellemzői! A vonzási tartományok fraktálszerű egymáshoz kapcsolódása konzisztens azzal az észrevétellel, hogy a kaotikus dinamikai rendszer időbeli fejlődése rendkívül érzékeny a kezdeti feltételekre, s ezért válik egy idő után indeterminisztikussá. Létezik egy olyan fázistérbeli ábra, amely a káoszelméletnek illetve a pillangóhatásnak később az ikonjává vált, ami nem is olyan véletlen, hiszen a görbesereg egy szárnyát kiterítő pillangóra emlékeztethet.

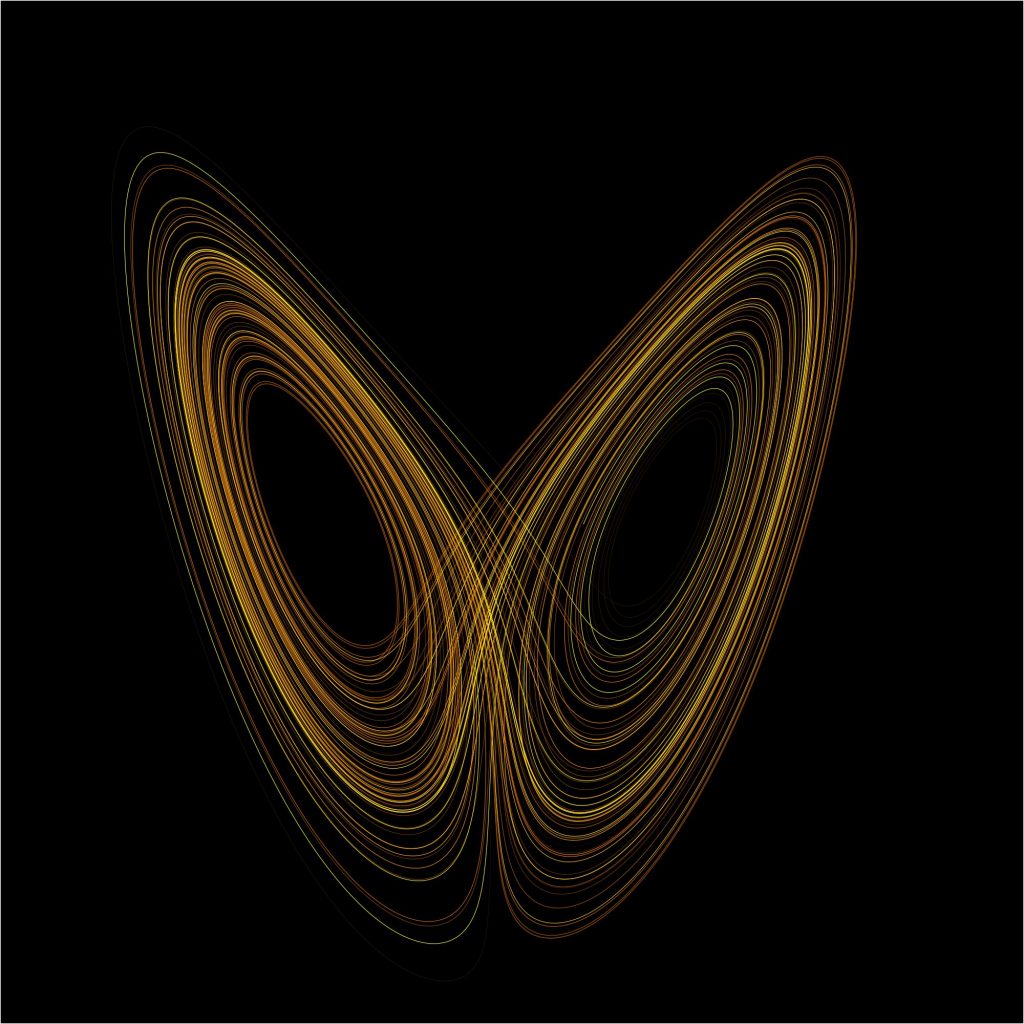
A görbéket Lorenz akkor kapta meg, amint a kezdeti feltételeket az időben elkezdte fejleszteni, majd a fázistérben ábrázolta azokat. Innen a neve ennek a különös attraktornak: Lorenz-attraktor. De miért is olyan különös ez az attraktor? Arról már volt szó, hogy az attraktorok vonzásközpontként működnek, innen eredeztethető a nevük is. Jelen esetben, ha a Lorenz által megfigyelt dinamikai rendszert bármilyen kezdőértékkel indítjuk el, nem látunk egy adott fix pontot, ami felé a fázistér pontjai tartanának. Azt is meg lehet figyelni, hogy nincsenek ismétlődő szakaszok benne, aperiodikus, tehát ez azt jelenti, hogy a dinamikai rendszer nem kerül kétszer ugyanabba az állapotába vissza. Továbbá azt is elmondhatjuk, hogy csak egy behatárolt területen belül rendelhető a dinamikai rendszerhez fázistérbeli pont, de mint fentebb említettem, nem fogja kétszer ugyanazt a trajektóriát bejárni a görbe. Ennek lesz az a következménye, hogy az attraktor fraktálszerű tulajdonságokat fog mutatni. Ezért is különös attraktor ez…

Térjünk vissza egy kicsit Lorenzhez, és képzeljük el azt, hogy a légkör állapotához egy ilyen fázistérbeli pontot rendelünk az időbeli fejlődése során. A kezdeti érték érzékenység miatt, ha nem végtelen pontossággal ugyanazokkal a paraméterekkel engedjük fejlődni a légkört leíró dinamikai rendszert, akkor merőben más állapotokhoz juthatunk el. Ez a fázistérbeli ábrán azt fogja eredményezni, hogy a különféle kezdeti értékekhez tartozó görbék divergálni fognak egymástól. Azt a furcsa megállapítást kell tenni, hogy egy kaotikus rendszer, egyszerre lesz kiszámíthatatlan, vagyis nem megjósolható és egyszerre determinisztikus. Kaotikussága érthető a számítások különböző eredményeiből, determinizmusa pedig abban áll, hogy a Newton-törvények szerint a jövőbeli világot a kezdeti kondíciók pontos ismeretében le lehet írni. Érdekes kettősség ez a newtoni keretrendszeren belül…

A tiszta determinizmus volt az, ami olyannyira megragadta  Pierre-Simon de Laplace francia fizikus és matematikus képzeletét, hogy egy Laplace démonja nevezetű képződménnyel igyekezett ennek a rendkívül szignifikáns kijelentésnek a következményeit boncolgatni. A híres tudós a következőket mondta:

„Felfoghatjuk a világunk jelenét úgy, mint a múltnak a következményét és a jövőnek az okát. Ha egy intellektus egy adott pillanatban ismerné a természetben található összes részecske helyzetét és sebességét, valamint a köztük fellépő erőhatásokat, és lenne olyan hatalmas kapacitása, hogy ezeket az adatokat befogadja és feldolgozza, akkor számára egy formulába lenne foglalva a legkisebb atomoktól a legnagyobb csillagokig minden testnek a mozgása. Egy ilyen intellektusnak semmi nem lenne bizonytalan vagy homályos, számára a jövő hasonlóan a múlthoz jelenként jelenne meg szemei előtt.”

-Pierre-Simon de Laplace francia fizikus-

A káosznak az a tulajdonsága, hogy a kis dolgok mennyire érzékenyen befolyásolják a nagyobb “képnek” az alakulását, számos ember képzeletét ragadta meg és olykor vezetett ez félreértésekhez a témán belül. Sokan elfelejtik, hogy a kiindulástól való rendkívüli érzékenység mindenképpen függést feltételez a két összehasonlítani kívánt esemény között. Ezért sem feltétlenül helytálló a Lorenz által is túlzásnak talált hasonlat a pillangóról és a forgószélről Texasban.

Úgy gondolom, érdekes lehet ennek a gondolatmenetnek a továbbvitele. Világunkban kétségtelenül tapasztalunk kaotikus rendszereket, elég egyedül a mágneses ingára gondolnunk, amit fentebb ismertettem. Egy kaotikus rendszer ismérve az, hogy a kiindulási differenciálegyenletek benne olyanok legyenek, melyek a kezdeti paraméterekre fokozottan érzékenyek. Ebből az következik, hogy ha egy rendszer kaotikus, annak egy szintén valamilyen kaotikus nagyobb rendszernek kell a részének lenni, hiszen egy nem kaotikus külső rendszer, nem válhat egyik pillanatról a másikra kaotikussá. A nem kaotikussága azt is jelentené a nagyobb rendszernek, hogy a kiinduló paraméterektől nincsen nemlineáris függése, azonban amint megjelenne benne egy kaotikus szakasz, ott már lenne. Ez így ellenmondásos, mert a kisebb rendszer nem tudna kaotikussá válni a lineárisan fejlődő külső rendszerbe ágyazottsága miatt.

A gondolatmenetet még tovább pörgetve, eljutunk oda, hogy a világunk végső soron kaotikus, vagyis a kezdeti értékek az Ősrobbanáskor (a későbbi természeti állandók) finomhangoltak. Ez azt jelenti, hogy ezeket a legapróbb mértékben is megváltoztatva olyan világ jött volna létre, ami merőben eltér a ma ismerttől, és akár az élet kialakulása sem lenne lehetséges benne.